Wasserstein距离与最优输运问题

Wasserstein距离是一种对于概率分布的距离度量，在某些类型的GAN生成模型中会使用到。其定义为：

$W(P, Q) = \inf_{\gamma∈\Pi(P,Q)} E_{(x,y)\sim\gamma} [\left\|x −y\right\|]$

其中 $\Pi(P,Q)$ 表示所有边缘分布为 $P,Q$ 的联合分布构成的集合。最开始看到这个定义的时候完全无法理解这是怎么来的，为什么要这样定义。其实这种距离与最优输运问题(optimal transport problem)相关。

考虑如下问题：有一堆石子以概率密度 $P$ 分布（不妨设分布在实数轴 $\mathbb R$ 上），我们需要通过移动这堆石子使得它的分布变成 $Q$ , 问如何以最小的代价做到这件事。

不妨将代价理解为搬运石头的重量乘以搬运距离。假如认为每个点处的石头不能分割运输，也就是说 $x$ 处的所有石头都得一起搬到 $T(x)$ 处，其中 $T(\cdot)$ 称为运输函数，那么总的搬运代价是：

$W(P, Q) = \inf_{T:T\#P=Q}\int_{\mathbb R} \left|x−T(x)\right|P(x)\text{d}x$

此处 $T\#P=Q$ 的含义是输运函数 $T$ 满足把分布 $P$ 变成分布 $Q$ ，或者更正式地说， $\forall B\subseteq \mathbb R, Q(B)=P(T^{-1}(B))$ .

但是在一些情况下，必须通过分割每个位置处的石块才能完成输运，例如初始有一块质量为2的石头位于原点，需要变成位于 $\pm1$ 位置的两块质量为1的石头，这时必须切成两块。在这种情况下，输运的代价就是最开始的那种形式了。

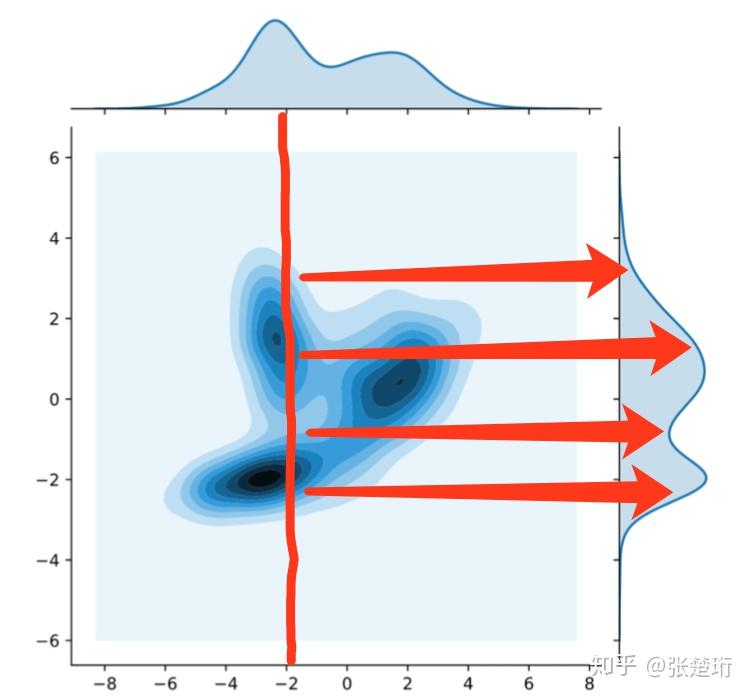
如何理解这件事情呢？从知乎上借来一张图：

假设最开始的分布 $P$ 是上面那样，我们把每一点的石头纵向“稀释”，然后再横向“收集”，使得最后的分布变为右侧那样的 $Q$ , 这其中的中间状态就是一个联合分布，满足边缘分布分别是 $P,Q$ ，从 $x$ 搬到 $y$ 的石头重量为 $\gamma(x,y)$ ，因此积分后就是上面那样。

取 $\inf$ 指的是对所有满足条件的输运函数 $T$ ，找一个做功最小的，然后这个最小代价就认为是分布 $P,Q$ 之间的距离，这有点类似于通过测地线定义抽象曲面上两个点距离的思想。直观来看，假如两个分布之间的最优输运过程需要的代价越大，两个分布的差异越大，因此这个距离定义合理。

参考文献